How to Code a Recursive Binary Search Function in Java

Intro

Recursion can be a very tricky concept to master, but it is so helpful in many different ways. In this article I will show you how to code a recursive binary search function. The binary search is an amazing search algorithm that searches for a number or an item in a list of those items and finds it in log(n) time. Normally, to find an item in an array you would need to search through the entire array and then see if any of them matches. In the worst case for this, you would search the entire array! Now, what if that array is sorted? We know that we don’t have to look through every item because that would be a waste of time. This is where the binary search algorithm comes in handy.

Given a sorted array, the binary search splits the array down the middle then determines whether to look farther ahead in the array, or farther back, then continues. This means that the absolute worst case, in which the item you are looking for is not in the array, or it is at the very end, it would only take log(n) time to find it! That is a massive cut on the time complexity of an unsorted array by searching linearly. Now there are methods to search those very quickly too which I will cover in later posts.

The Code

Now, the way I start any function is by looking at what goes in, and what comes out. We want our function to return a boolean, whether the item is in the array or not, and we want to give it the lowest index, the highest index, the item we are looking for, and the array. Now, with all this in mind we can draw out the bones of our function. Here is what we have so far:

public static boolean recursiveSearch(int target, int[] array, int low, int high)
{
  return false;
}

I made my function static because it is being called from a static function, and the way Java works is that it only allows you to call a static function in the same class from another static function. Anyways, we have our function return a boolean, and it’s input is the low and the high index, the array, and the target. Great! Now we want to think about how to code this.

Since this is a recursive function we want to know what our base case is. The base case is what our function will ultimately end up at and cause the recursion to stop. Since we are splitting the array down the middle, and either low or high will be changing, we can say: when low is greater than high, return false. This means we have searched the entire array and not found what we are looking for, so it is OK to exit the search with a false value. Here’s the code:

public static boolean recursiveSearch(int target, int[] array, int low, int high)
{
  if(low > high)
    return false;

  return false;
}

The return false on the bottom is for the Java syntax which requires a value to be returned no matter what. Now that we have this in we can get the real coding done. We want our function to first split the array down the middle, so we can simply say the middle is equal to low plus high divided by two. This will split our search area in two halves with the center as close to the center as possible.

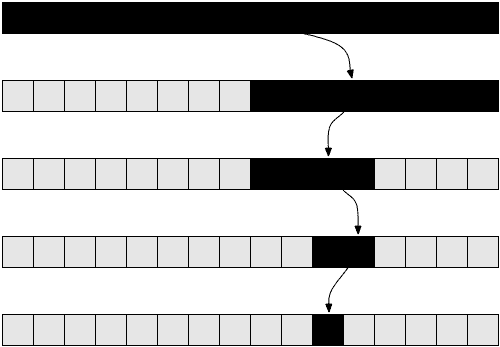
After we find the middle index we have three cases, either the middle is the number we are looking for, it is greater than the number we are looking for, or it is less than the number we are looking for. If it is greater than the number we are looking for we want to search the left half of the search area for our number, if it is greater than the number, we want to search the right half, etc. Here’s a diagram showing what’s going on:

As you can see the black is the search area, if the element is greater the search area splits to the right half, if it is less it splits to the left half. We are simply doing this in code. Now let’s program what this would look like:

public static boolean recursiveSearch(int target, int[] array, int low, int high)
{
  if(low > high)
    return false;
  else
  {
    int mid = (low + high) / 2;
    if(target == array[mid])
      return true;
    else if(target < array[mid])
      return false // TODO
    else if(target > array[mid])
      return false // TODO
  }

  return false;
}

So right there we have programmed it to say if the target is equal to the middle element, return true because we have found it. If the target is less than the element do something, and if it is greater than the element do something else. Now since this is a recursive function we want to call it in both of those else if statements. The way we want to call it is by calling it and modifying either low or high. When we modify the low index or the high index we are changing the bounds of the search area. So we will simply call the same function with a modified search area, it will look like this:

public static boolean recursiveSearch(int target, int[] array, int low, int high)
{
  if(low > high)
    return false;
  else
  {
    int mid = (low + high) / 2;
    if(target == array[mid])
      return true;
    else if(target < array[mid])
      return recursiveSearch(target, array, low, mid - 1);
    else if(target > array[mid])
      return recursiveSearch(target, array, mid + 1, high);
  }

  return false;
}

Now that should all make sense, the only thing you may be wondering is why the -1 and +1. Well, if you were to search for the element on the very left, you would never reach it if you simply passed in mid. The reason is because the middle would never reach that left point because it would constantly be picking the element right next to it! If you don’t believe me remove the -1 and the +1 and watch what happens.

The way to call the function above would look like this, and you would place this inside the main function of your program:

...
recursiveSearch(450, arrayOfNumbers, 0, arrayOfNumbers.length - 1)
...

So I hope this helps shed some light on how to program a recursive function that searches an array using a binary split. Good luck programming, and if you have questions or comments submit them below!